What is a quadrilateral? Understand types & properties
The geometric figures give us different ways that can be taken so that we will be able to explain the formula and the calculations as well. As such the geometrical figures do not only make the calculations easy but also at the same will help us make the representations easier as well.
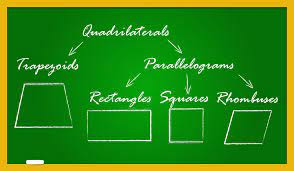
In the general terms, a quadrilateral is being defined as a plane figure that has four sides or edges, and also has four corners or vertices. Quadrilaterals will typicallydefined as to be of standard shapes with four sides like rectangle, square, trapezoid, and kite or irregular and uncharacterized as shown below:
Types of Quadrilaterals
There are many types of quadrilaterals. As we can see here that the term ‘Quad’ means four, all these types of a quadrilateral have four sides, and the sum of angles of these shapes is 360 degrees.
- Trapezium
- Parallelogram
- Squares
- Rectangle
- Rhombus
- Kite
There will be yet another way that we can classify the types of quadrilaterals is:
- Convex Quadrilaterals: in this, we have both the diagonals of a quadrilateral thatare completely contained within a figure.
- Concave Quadrilaterals: in this we have at least one of the diagonals that lie partlyand are entirely outside of the figure.
- Intersecting Quadrilaterals: Intersecting thequadrilaterals are not simple quadrilaterals in which the pair of non-adjacent sideswill intersect. This kind of quadrilaterals is alsoknown as self-intersecting or crossed quadrilaterals.
Quadrilateral Formula
Area of the quadrilateral is to be calculated as the total space occupied by the figure. The area formula for the different quadrilaterals is given below:
| Area of a Parallelogram | Base x Height |
| Area of a Rectangle | Length x Width |
| Area of a Square | Side x Side |
| Area of a Rhombus | (1/2) x Diagonal 1 x Diagonal 2 |
| Area of a Kite | 1/2 x Diagonal 1 x Diagonal 2 |
Quadrilateral Properties
Now that we have gathered a general information of the different types of the of types of the quadrilateral let us try and understand the properties of each one of them.
- There are four sides: that are AB, BC, CD, and DA
- There will be four vertices: the Pointsare A, B, C, and D
- Four angles are defined as :∠ABC, ∠BCD, ∠CDA, and ∠DAB
- ∠A and ∠B are adjacent angles whereas ∠A and ∠C are the opposite angles
We will notice that for each quadrilateral we have 4 vertices, 4 angles, and 4 sides and the total of its interior angles = 360 degrees
Square Properties
- In the square , all the sides of the square are of equal measure and the sides are parallel to each other
- In this figure, we will find that the interior angles of a square are at 90 and the diagonals of a square perpendicular bisect each other
Rectangle Properties
- In this type of figure ,opposite sides of a rectangle are of equal length and the opposite sides are parallel to each other
- All the interior angles of a rectangle will be at 90 degrees and the diagonals will bisect each other.
Rhombus Properties
- All the four sides of a rhombus are of the same measure
- The opposite sides of the rhombus are parallel to each other
- The opposite angles are of the same measure
- The sum of any two adjacent angles of a rhombus is equal to 180 degrees
- The diagonals perpendicularly bisect each other
Parallelogram Properties
- The opposite side of the parallelogram will be of same length and the opposite side parallel.
- The diagonals of a parallelogram will bisect each other and the opposite angles are equal.
- If we add the two adjacent angles of a parallelogram then the sum is equal to 180 degrees
Properties of Trapezium
- In this figure only one pair of the opposite side of a trapezium is parallel to each other
- We will have the two adjacent sides of a trapezium be supplementary.
- When we draw the diagonals of a trapezium they will bisect each other in the same ratio
Properties of Kite
- The pair of adjacent sides of a kite will be of the same length
- In the kite, the largest diagonal of a kite bisect the smallest diagonal
- We will have only one pair that will be equal.
For more solved examples and doubt clearance, use online learning app.













